Θέση-Μετατόπιση. Φύλλο εργασίας.

Να τονίσουμε αρχικά ότι η θέση ενός υλικού σημείου ορίζεται πάντα ως προς ένα ορισμένο σύστημα αναφοράς. Για παράδειγμα για να δώσουμε την θέση μιας μπάλας Σ, την καθορίζουμε σε σχέση με κάποιο γνωστό σημείο. Στο παρακάτω σχήμα η θέση της μπάλας ως προς το μάτι Ο, ενός παρατηρητή, καθορίζεται από το διάνυσμα r.

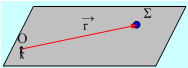
Για να ορίσουμε δε τη θέση του, σχεδιάζουμε ένα διάνυσμα το οποίο έχει αρχή το σημείο αναφοράς (συνήθως την αρχή Ο ενός συστήματος αξόνων xy, για μια θέση πάνω στο επίπεδο xy) και τέλος τη θέση του υλικού σημείου.

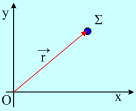
Αν τώρα το σώμα μας μετακινείται και πηγαίνει από μια θέση Α σε άλλη Β, ορίζουμε την μεταβολή της θέσης του ή αλλιώς μετατόπισή του, η οποία είναι επίσης διάνυσμα με αρχή την αρχική θέση Α και τέλος την τελική θέση Β.


1) Με βάση τα παραπάνω, ένα κινητό μετακινείται πάνω σε ένα οριζόντιο επίπεδο και στο σχήμα φαίνονται οι διαδοχικές θέσεις από τις οποίες διέρχεται (η τροχιά του) πηγαίνοντας από την θέση Α στη θέση Β.

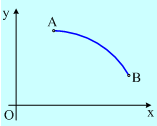
i) Να σχεδιάστε τα διανύσματα της αρχικής θέσης, της τελικής θέσης του και της μετατόπισής του.
ii) Να σχεδιάστε τα αντίστοιχα διαγράμματα ως προς το σύστημα αναφοράς x΄Ο΄y΄.

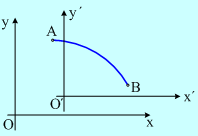
Απάντηση:


2) Έστω τώρα ότι ένα υλικό σημείο μετακινείται από τη θέση Α στη θέση Β, όπου η μετακίνηση γίνεται πάνω σε ευθεία γραμμή. Προσανατολίζουμε την ευθεία και ορίζουμε το σημείο Ο, σαν αρχή του άξονα x.

Να σχεδιάστε τα διανύσματα της αρχικής θέσης, της τελικής θέσης του και της μετατόπισης του σώματος.


3) Σχεδιάστε επίσης τα ίδια διανύσματα στην παρακάτω περίπτωση:



4) Ας το ξανακάνουμε στο παρακάτω σχήμα.



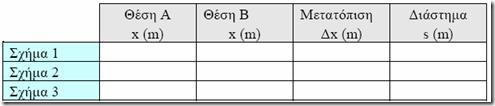
5) Να συμπληρωθεί ο παρακάτω πίνακας με τις αλγεβρικές τιμές για τις θέσεις του σώματος, την αλγεβρική τιμή της μετατόπισης και το διάστημα που διανύει το σώμα στα σχήματα 1,2 και 3.
Υπενθυμίζεται ότι, από τη στιγμή που ένα διανυσματικό μέγεθος είναι πάνω στον γνωστό άξονα x, γνωρίζουμε την διεύθυνσή του, συνεπώς μας αρκεί ένας αριθμός (θετικός ή αρνητικός) για να μας δείξει το μέτρο του και την κατεύθυνσή του. Ο αριθμός αυτός ονομάζεται αλγεβρική τιμή του μεγέθους.
Για παράδειγμα στο παρακάτω σχήμα:

Το διάνυσμα α έχει μήκος 7m, συνεπώς το μέτρο του είναι 7m και επειδή έχει φορά προς τ’ αριστερά η αλγεβρική του τιμή είναι α=-7m.





Μπορείτε να κατεβάσετε το αρχείο σε pdf.