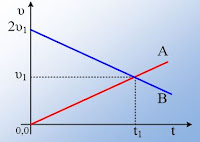
Στο φανάρι ενός ευθύγραμμου δρόμου, το οποίο έχει ανάψει
κόκκινο, βρίσκονται ακίνητα δύο αυτοκίνητα Α και Β. Τη στιγμή που το φανάρι
γίνεται πράσινο (t0=0), ο οδηγός του Α αυτοκινήτου του προσδίδει
σταθερή επιτάχυνση μέτρου α1=2m/s2, με την οποία
κινείται. Αντίθετα ο οδηγός του Β αυτοκινήτου ήταν αφηρημένος και καθυστέρησε
την εκκίνηση για 4s, ενώ στη συνέχεια προσέδωσε σταθερή επιτάχυνση στο όχημά
του α2=3m/s2. Θεωρούμε τη θέση του φαναριού ως αρχή ενός
προσανατολισμένου άξονα x, με θετική φορά προς τα δεξιά.
i) Να δοθούν οι εξισώσεις της ταχύτητας υΑ(t)
και της θέσης xΑ(t) για το αυτοκίνητο Α και να βρείτε την θέση και
την ταχύτητά του τη στιγμή t1=4s.
ii) Να
γραφτούν οι αντίστοιχες εξισώσεις ταχύτητας υΒ(t) και της θέσης xΒ(t)
για το αυτοκίνητο Β.
iii)
Υποστηρίζεται ότι μόλις ξεκινήσει το Β αυτοκίνητο, η απόσταση μεταξύ των δύο
οχημάτων θα αρχίσει να μειώνεται, μιας και αυτό αποκτά μεγαλύτερη επιτάχυνση
από το Α. Μπορούμε να ελέγξουμε την παραπάνω υπόθεση με δυο τρόπους.
α) Να
υπολογίσουμε τη μετατόπιση κάθε αυτοκινήτου για χρονικό διάστημα Δt=2s, μετά
την εκκίνηση του δεύτερου. Σε τι συμπέρασμα καταλήγετε;
β) Να
βρούμε τις θέσεις των δύο οχημάτων τη χρονική στιγμή t2=6s. Πόση
είναι η απόσταση μεταξύ των δύο αυτοκινήτων τη στιγμή αυτή; Να συγκριθεί με την
μεταξύ τους απόσταση τη στιγμή t1.
iv) Να
βρεθεί ποια χρονική στιγμή t3 τα δύο αυτοκίνητα κινούνται με την
ίδια ταχύτητα u. Τη στιγμή αυτή να βρεθούν οι ταχύτητες και οι θέσεις των δύο
αυτοκινήτων. Πόση είναι η απόσταση μεταξύ των δύο αυτοκινήτων τη στιγμή αυτή;
v) Να
υπολογιστεί η απόσταση μεταξύ των δύο αυτοκινήτων τη στιγμή t4=t3+2s.
Μπορείτε να βγάλετε κάποιο συμπέρασμα για το τι γίνεται με την απόσταση των δύο
αυτοκινήτων, στη διάρκεια των παραπάνω κινήσεων;
ή