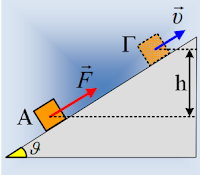
Ένα σώμα μάζας 2kg ηρεμεί στη θέση Α ενός λείου οριζοντίου επιπέδου,
απέχοντας κατά x=0,5m από τη βάση (σημείο Γ) ενός λείου κεκλιμένου επιπέδου κλίσεως
θ. Κάποια στιγμή ασκούμε στο σώμα μια οριζόντια σταθερή δύναμη F, με αποτέλεσμα
το σώμα να φτάνει στη θέση Γ με ταχύτητα μέτρου υ1=2m/s. Στη
συνέχεια το σώμα συνεχίζει την κίνησή του κατά μήκος του κεκλιμένου, μέχρι να
μηδενιστεί στιγμιαία η ταχύτητά του αφού διανύσει απόσταση s=2m (θέση Δ), ενώ η
δύναμη F, άλλαξε διεύθυνση, παίρνοντας τη διεύθυνση του επιπέδου, διατηρώντας
σταθερό το μέτρο της. Να υπολογιστούν:
i) Η ενέργεια που μεταφέρθηκε στο σώμα μέσω του έργου
της δύναμης στη διαδρομή ΑΓ, καθώς και το μέτρο της δύναμης F.
ii) Η γωνία κλίσεως θ του επιπέδου.
iii) Η μέγιστη αύξηση της δυναμικής ενέργειας του
σώματος στη διαδρομή ΑΔ και να συγκριθεί με το έργο της δύναμης F.
iv) Μόλις μηδενιστεί η ταχύτητα στη θέση Δ, η δύναμη F
παύει να ασκείται στο σώμα. Να βρεθεί η μέγιστη ταχύτητα που αποκτά στη
συνέχεια το σώμα.
Δίνεται
g=10m/s2.
ή
 | Ένα σώμα παίρνει την ανηφόρα |