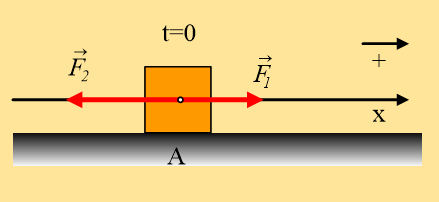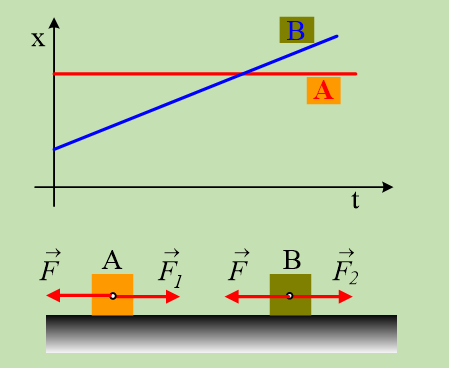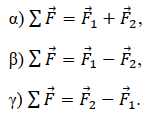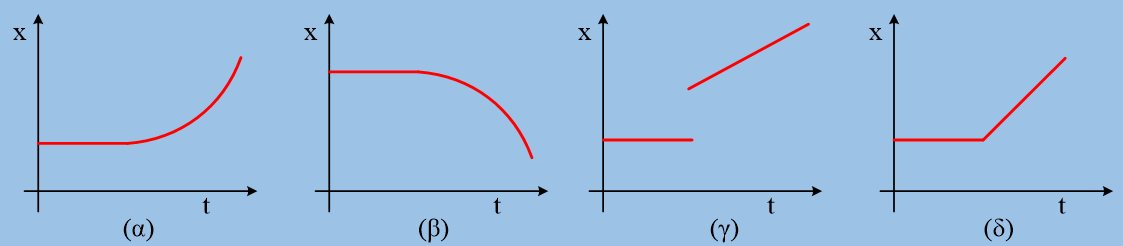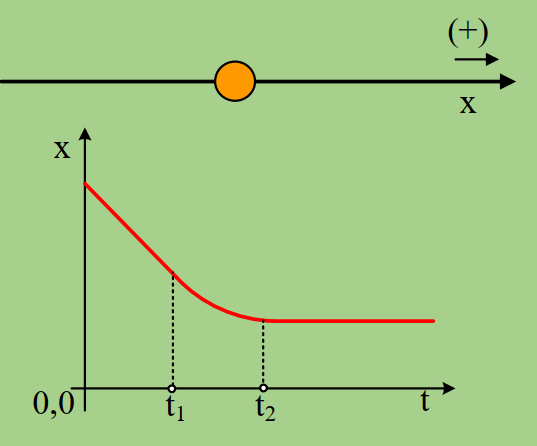
Μια μικρή σφαίρα κινείται σε λείο οριζόντιο επίπεδο κατά μήκος ενός προσανατολισμένου άξονα x και στο σχήμα δίνεται η θέση της σφαίρας σε συνάρτηση με το χρόνο. Στη σφαίρα μπορεί να ασκείται μια μόνο οριζόντια δύναμη στη διεύθυνση x.
i) Μπορείτε να περιγράψετε την κίνηση της σφαίρας με βάση το διάγραμμα αυτό;
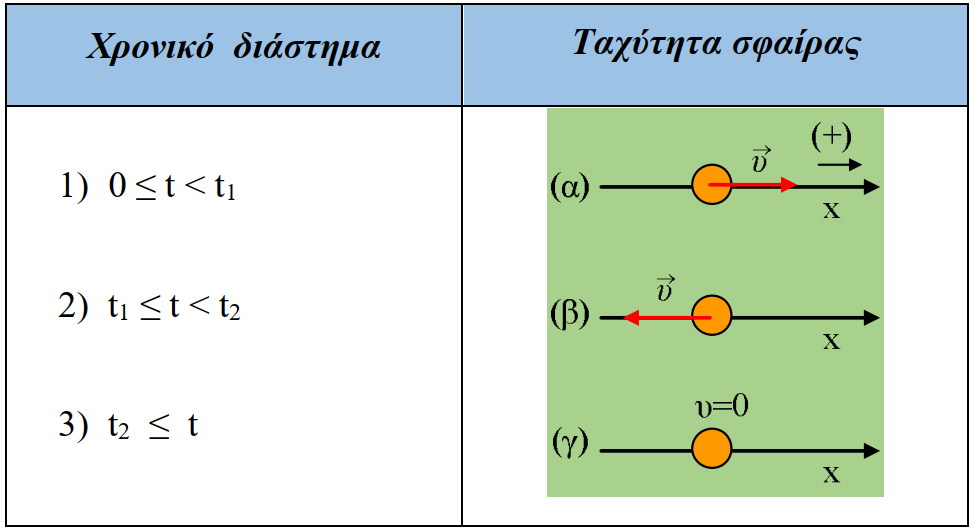
ii) Στον παρακάτω πίνακα εμφανίζονται τα διάφορα χρονικά διαστήματα και στην διπλανή στήλη έχει σχεδιαστεί η πιθανή ταχύτητα της σφαίρας. Να κάνετε τις αντιστοιχίσεις και στη συνέχεια να δοθεί και σύντομη ερμηνεία.
iii) Ποιες οι αντίστοιχες αντιστοιχίσεις μεταξύ χρονικών διαστημάτων και του σχήματος που δείχνει την ασκούμενη οριζόντια δύναμη που μπορεί να ασκείται στη σφαίρα;
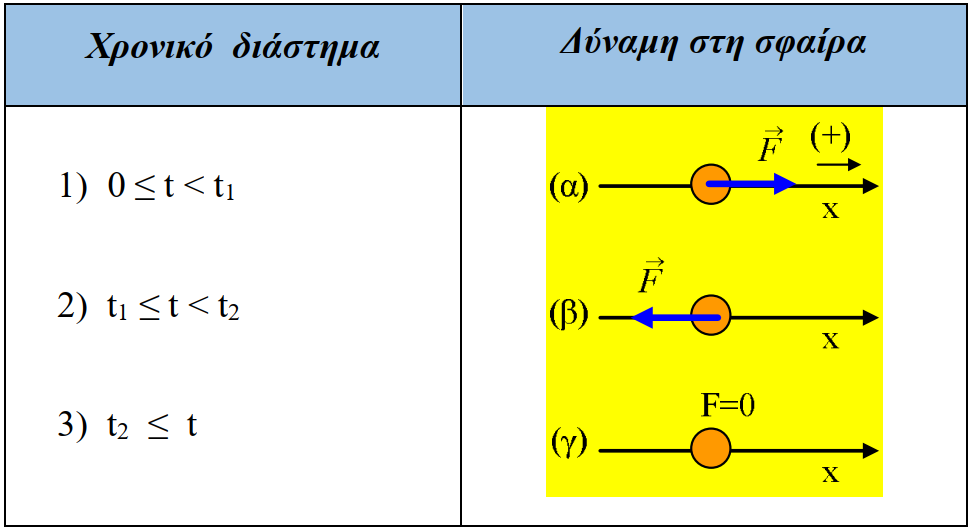
Να δικαιολογήσετε τις επιλογές σας.